Jörn Alexander Quent's notebook

where I share semi-interesting stuff from my work

Understanding the basics of the general linear model (GLM) in the context of fMRI

in  experiments  , ,

Prelude

I was revisiting some of the basics surrounding fMRI especially the GLM and contrasts. I’ve tried to find code examples and equations but I didn’t really find anything for R. While I found the accessible explanations and equations in Poldrack et al. (2011) and more advanced concepts in Kutner (2005), I didn’t find code examples. So in the spirit of Heinrich von Kleist, who pointed out your understanding will get much better if you try to explain things yourself, I am creating minimalist code examples myself while showing that those fit the results that I get from R’s built-in functions (e.g. t-tests).

Note I am not expert in this field and I might have gotten some terminology or equations wrong. If you find a mistake please find my e-mail and tell me about it. Think of this as me sharing my cheat sheet, which I would use when ever I have to refresh my knowledge. I am sharing this because I thought some one else might get stuck (like me) trying to understand some of the concepts. For details I first recommend taking a look at Poldrack’s book (especially the appendix) and then Kutner. Generally, the examples used here are only illustrations and might not be the best approximations of actual brain data (e.g. smoothness etc.).

Last note: The contrasts and design matrices are only valid for the exact ordering of the data so you can only use those if your ordering of the data is the same.

Sources that I found useful

General libraries

# Install via devtools::install_github("JAQuent/assortedRFunctions", upgrade = "never")
library(assortedRFunctions)
library(Matrix)
library(lattice)
library(soundgen)
library(cowplot)
library(ggplot2)
library(knitr)

Simple linear regression

Starting off with something very easy: simple linear regression as viewed through the GLM-framework. I start with generating fake data.

# Set seed
set.seed(102)

# Fake data parameters
n     <- 100
beta0 <- 2
beta1 <- 5

# Create fake data
x <- runif(n)
Y <- matrix(rnorm(n, beta0 + beta1*x, 1), ncol = 1)

# Plot data
plot(x, Y)

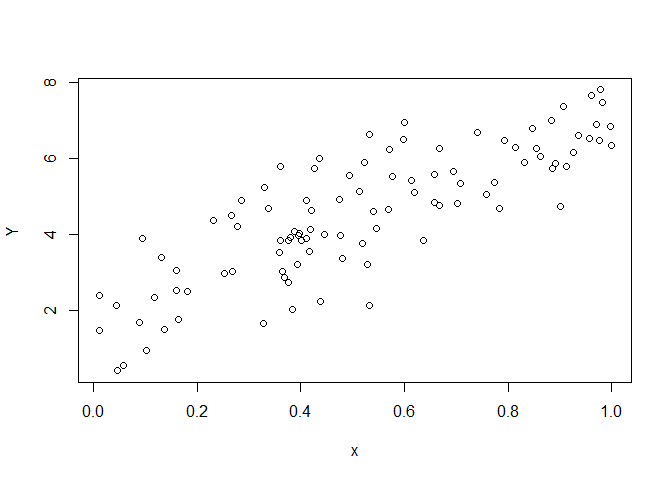
The data is illustrated in a scatter plot. When analysing the data using lm() I get the following results

# Analysis using lm()
lm_model <- lm(Y ~ x)
summary(lm_model)

## 
## Call:
## lm(formula = Y ~ x)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.49576 -0.61718 -0.08426  0.60519  2.07532 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   1.8667     0.2093   8.918 2.69e-14 ***
## x             5.1762     0.3560  14.540  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9751 on 98 degrees of freedom
## Multiple R-squared:  0.6833, Adjusted R-squared:   0.68 
## F-statistic: 211.4 on 1 and 98 DF,  p-value: < 2.2e-16

which gives me an estimate of the intercept & slope.

The equation corresponding to the model above can be expressed as

$$ Y = \beta_{0}+ \beta_{1}x_{1}+\epsilon $$ the model fit to the data via lm() estimated that $\beta_0$ = 1.8667 and $\beta_1$ = 5.1762.

While, the model equation is useful in some ways (e.g. easy to understand) it is also highly specific and only pertains to models that exactly like this one, which have an intercept and a slope. When conceptualising everything in the GLM-framework, we can do something much more powerful as we can generally write this model as

$$ Y = X\beta + \epsilon $$

which is the a valid description for all the different kinds of models & tests that fall under the GLM umbrella. Therefore we can use the same notation and tricks to deal with a wide variety of statistical problems. All that we have to do to analyse data following this notation is to create the design matrix $X$.

# Calculate the design matrix 
X <- matrix(c(rep(1, n), x), ncol = 2)

# Visualise design matrix
dispDesignMatrix(X)
title(main = 'Simple linear regression design matrix')

In the simple example above our design matrix has 1s for the intercept (i.e. $\beta_0$) and the values of our variable $x$ for the second column representing $\beta_1$.

When we have this, estimating the $\beta$s is very simple, assuming that $X^\intercal X$ is invertible (for an inverse of $X^\intercal X$ to exists $X$ must have full column rank, see Glossary for explanation or the YouTube video that I added), using this equation:

$$ \hat{\beta} = (X^\intercal X)^{-1} X^\intercal Y$$

Note that is what we get if we premultiply $Y = X\beta + \epsilon$ by $X^\intercal$:

$$ X^\intercal Y = X^\intercal X\beta$$ which is a neat trick that allows us to invert the matrix.

In R this would look like this:

# Estimate betas via Ordinary Least Squares (OLS) estimation
B <- solve(t(X)%*% X) %*% t(X) %*% Y

Fortunately, using this equation we get the same values for $\beta_0$ = 1.8667 and $\beta_0$ = 5.1762.

Quick side note: solve() can only invert matrices that are square (e.g. 3 x 3) directly

$$ A = \begin{bmatrix} 2 & 5 & 3 \ 4 & 0 & 8 \ 1 & 3 & 0 \end{bmatrix} $$

in this case

$$ A^{-1} = solve(A) = (A^\intercal A)^{-1} A^\intercal$$

A          <- matrix(c(2, 4, 1, 5, 0, 3, 3, 8, 0), ncol = 3)
A_inverse1 <- solve(A)
A_inverse2 <- solve(t(A)%*% A) %*% t(A)
# Note A_inverse1 == A_inverse2 actually returns FALSE but the values are the same, which is due to rounding.

So the trick of transposing and then multiplying the matrix with itself is something we have to use because our design matrix $X$ are typically not square.

Moving on, estimates for $Y$ can be calculated like this

$$ \hat{Y} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{1}$$

or in matrix notation

$$ \hat{Y} = X\beta $$

In R this works simply by

Y_hat <- X %*% B

The residuals can be obtained like this

$$ e = Y - \hat{Y} $$

E <- Y - Y_hat

To calculate the test statistics like $t$ we also need an estimation of the variance of the residuals

$$ \hat{\sigma}^2 = \frac{e^\intercal e}{N-p} $$ where $N$ is the number of rows and $p$ is the number of columns of the design matrix $X$.

p <- ncol(X)
N <- nrow(X)
resid_var <- as.numeric((t(E) %*% E)/(N-p))

In our case $\hat{\sigma}^2$ is 0.9508.

With the help of contrasts that are row-vectors with length $p$ we can test hypotheses as t-tests (or even as F-tests).

For instance, if we want to test if the intercept ($\beta_0$) is zero i.e. $H_o: \beta_0 = 0$, we can use the following contrast

$$ con_1 = \begin{bmatrix} 1 & 0\end{bmatrix}$$ If we want to test if our slope ($\beta_1$) is zero i.e. $H_o: \beta_1 = 0$, we use the following contrast:

$$ con_2 = \begin{bmatrix} 0 & 1\end{bmatrix}$$ Both hypotheses can be expressed more generally as $H_0: c\beta =0$. In R, we simply need to do

con1 <- matrix(c(1, 0), ncol = 2)
con2 <- matrix(c(0, 1), ncol = 2)

The $t$-statistic is then calculated by

$$ t = \frac{con\hat{\beta}}{\sqrt{con(X^\intercal X)^{-1}con^\intercal \hat{\sigma}^2} }$$

This looks more scary then it is. The numerator in case for $con_1$ is simply our $\beta_0$ estimate.

numerator <- con1 %*% B

$c_1\hat{\beta}$ = 1.8667. The denominator is the standard error of the estimate. Which can be calculated by

denominator <- sqrt(con1 %*% solve(t(X)%*% X) %*% t(con1) * resid_var)

so $\sqrt{con_1(X^\intercal X)^{-1}con_1^\intercal \hat{\sigma}^2}$ is 0.2093.

t1 <- numerator/denominator

So like above when calculated with lm() $t$ = 8.9182.

Just to demonstrate, we also get the correct values for our second contrast:

numerator   <- con2 %*% B
denominator <- sqrt(con2 %*% solve(t(X)%*% X) %*% t(con2) * resid_var)
t2          <- numerator/denominator

$t$ = 14.54.

Multiple linear regression

Within the GLM-framework, we can also run multiple regression models and most importantly F-tests.

# Set seed
set.seed(102)

# Fake data parameters
n     <- 100
beta0 <- 2
beta1 <- 5
beta2 <- 0.4
beta3 <- -4

# Create fake data
x1 <- runif(n)
x2 <- runif(n)
x3 <- runif(n)
Y  <- matrix(rnorm(n, beta0 + beta1*x1 + beta2*x2 + beta3*x3, 1), ncol = 1)

# Analysis using lm()
lm_model <- lm(Y ~ x1 + x2 + x3)
summary(lm_model)

## 
## Call:
## lm(formula = Y ~ x1 + x2 + x3)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.2840 -0.6754 -0.0352  0.7310  2.2748 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   2.2686     0.3515   6.454 4.43e-09 ***
## x1            4.6536     0.3740  12.442  < 2e-16 ***
## x2            0.2280     0.3633   0.628    0.532    
## x3           -4.0781     0.3800 -10.732  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.02 on 96 degrees of freedom
## Multiple R-squared:  0.741,  Adjusted R-squared:  0.7329 
## F-statistic: 91.55 on 3 and 96 DF,  p-value: < 2.2e-16

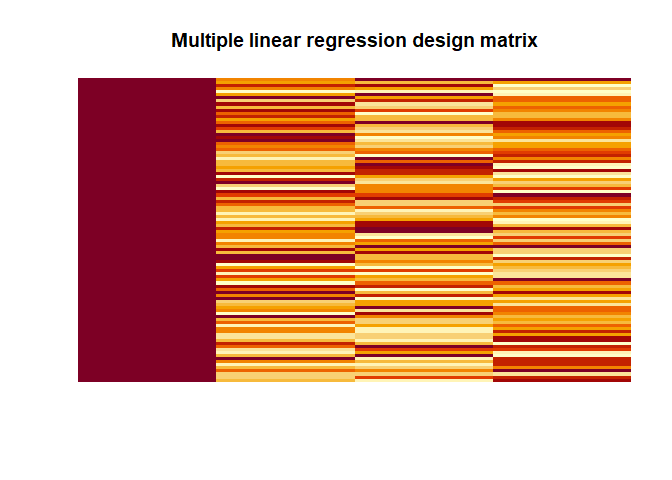
# Calculate the design matrix 
X <- matrix(c(rep(1, n), x1, x2, x3), ncol = 4)

# Visualise design matrix
dispDesignMatrix(X)
title(main = 'Multiple linear regression design matrix')


# Estimate betas via Ordinary Least Squares (OLS) estimation
B <- solve(t(X)%*% X) %*% t(X) %*% Y

Again we get the same values as with lm() 2.2686, 4.6536, 0.228, -4.0781.

If we want to test $H_0: \beta_1 = \beta_2 = \beta_3 = 0$ or in other words if any of the $\beta$s that are not the intercept are different from zero, then we can use the following contrast:

$$ con = \begin{bmatrix} 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1\end{bmatrix} $$

# Quick & dirty way to create the contrast is to remove the first row of an identity matrix
con <- diag(4)
con <- con[-1,]

The test statistics is then calculated by

$$ F = (con\hat{\beta})^\intercal [rcon(\hat{Cov}(\hat{\beta}))con^\intercal]^{-1}(con\hat{\beta})$$

where $r$ is the rank of the contrast matrix/vector $con$,

r <- as.numeric(rankMatrix(con))

which in our case is 3 as there are 3 independent columns in $con$ and

$$ \hat{Cov}(\hat{\beta}) = (X^\intercal X)^{-1}\hat{\sigma}^2 $$

Now we can calculate our F-value by hand:

# Calculate residual variance
Y_hat <- X %*% B
E <- Y - Y_hat
p <- ncol(X)
N <- nrow(X)
resid_var <- as.numeric((t(E) %*% E)/(N-p))

# Covariance of beta
Cov_hat_beta <- solve(t(X) %*% X) * resid_var

# Calculate F- test
F_stat <- t(con %*% B) %*% solve(r * con %*% Cov_hat_beta %*% t(con)) %*% (con %*% B)

In this case, $F$ = 91.5454, which can matches the one that lm() spits out.

Special cases

The GLM is also powerful not only for the these regression models but also for a number of special cases that we often use for imaging.

One sample t-test

# Fake data parameters
n     <- 100
beta0 <- 2
beta1 <- 5

# Create fake data
x <- runif(n)
Y <- matrix(rnorm(n, beta0 + beta1*x, 1), ncol = 1)

# Create design matrix
X <- matrix(c(rep(1, n)), ncol = 1)

# Estimate betas
B <- solve(t(X)%*% X) %*% t(X) %*% Y

# Calculate residual variance
Y_hat <- X %*% B
E <- Y - Y_hat
p <- ncol(X)
N <- nrow(X)
resid_var <- as.numeric((t(E) %*% E)/(N-p))

# Contrast
con <- 1

# Calculate the t value
numerator   <- con %*% B
denominator <- sqrt(con %*% solve(t(X)%*% X) %*% t(con) * resid_var)
t_value     <- numerator/denominator

In this model $\beta_1 = mean(Y)$ = 4.4319552. As calculated when we use t.test(), the $t$-value is 26.2878. $H_0: \beta_1 = 0$.

t.test(Y)

## 
##  One Sample t-test
## 
## data:  Y
## t = 26.288, df = 99, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  4.097429 4.766481
## sample estimates:
## mean of x 
##  4.431955

Two sample t-test

# Generate new data
y1 <- rnorm(n, 0)
y2 <- rnorm(n, 0.3)
Y  <- c(y1, y2)

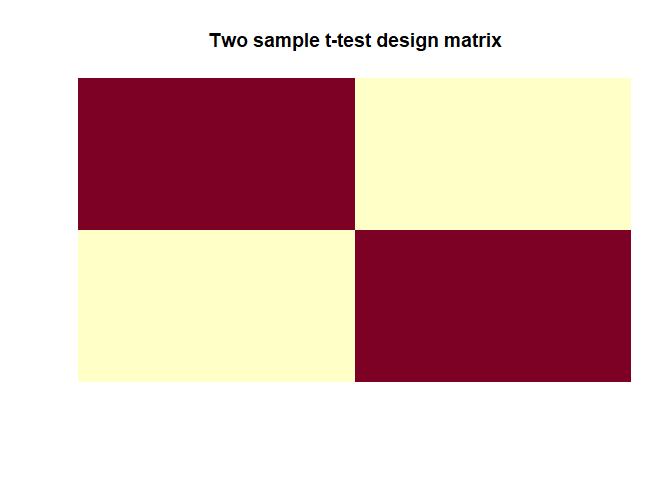
# Create design matrix
X <- matrix(c(rep(c(1,0), each = n), rep(c(0,1), each = n)), ncol = 2)

# Display design matrix
dispDesignMatrix(X)
title(main = 'Two sample t-test design matrix')


# Estimate betas
B <- solve(t(X)%*% X) %*% t(X) %*% Y

# Calculate residual variance
Y_hat <- X %*% B
E <- Y - Y_hat
p <- ncol(X)
N <- nrow(X)
resid_var <- as.numeric((t(E) %*% E)/(N-p))

# Contrast
con <- matrix(c(1, -1), ncol = 2)

# Calculate the t value
numerator   <- con %*% B
denominator <- sqrt(con %*% solve(t(X)%*% X) %*% t(con) * resid_var)
t_value     <- numerator/denominator

In this model $\beta_1 = mean(y_1)$ and $\beta_2 = mean(y_2)$ which are -0.0807, 0.2204 (the group averages). As calculated with t.test(), the $t$-value is -2.3043. $H_0: \beta_1 - \beta_2 = 0$.

t.test(y1, y2, var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  y1 and y2
## t = -2.3043, df = 198, p-value = 0.02224
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.55875369 -0.04341614
## sample estimates:
##   mean of x   mean of y 
## -0.08068517  0.22039974

Paired t-test

# Fake data
n  <- 20
y1 <- rnorm(n, 0)
y2 <- rnorm(n, 0.3)
Y  <- rep(0, n * 2)
Y[seq(from = 1, to = n*2, by = 2)] <- y1
Y[seq(from = 2, to = n*2, by = 2)] <- y2
id <- rep(1:n, each = 2)

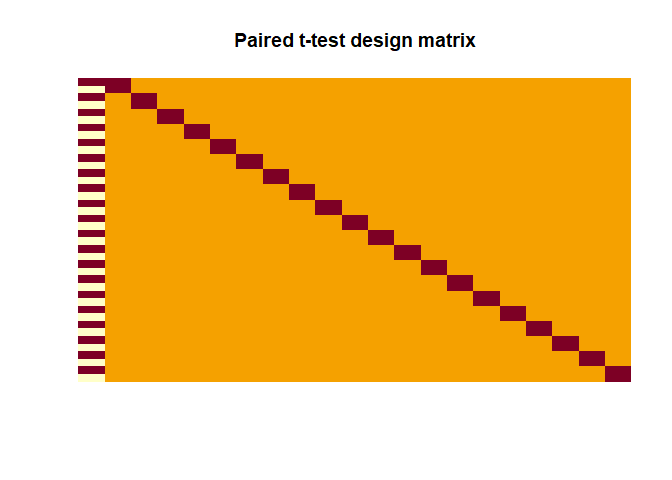
# Create design matrix
X <- matrix(0, ncol = n + 1, nrow = n*2)
# Change first column
X[, 1] <- rep(c(1, -1), n)
# Loop through X
for(i in 1:n){
  X[which(id == i), i + 1] <- 1
}

# Display design matrix
dispDesignMatrix(X)
title(main = 'Paired t-test design matrix')


# Estimate betas
B <- solve(t(X)%*% X) %*% t(X) %*% Y

# Calculate residual variance
Y_hat <- X %*% B
E <- Y - Y_hat
p <- ncol(X)
N <- nrow(X)
resid_var <- as.numeric((t(E) %*% E)/(N-p))

# Contrast
con <- matrix(c(1, rep(0, n)), ncol = n + 1)

# Calculate the t value
numerator   <- con %*% B
denominator <- sqrt(con %*% solve(t(X)%*% X) %*% t(con) * resid_var)
t_value     <- numerator/denominator

Here the contrast has to be

$$ con = \begin{bmatrix} 1 & 0 & 0 & 0 & \cdots & 0\end{bmatrix}$$ in order to test $H_0: \beta_{diff} = 0$. As calculated with t.test(), the $t$-value is 0.2388.

t.test(y1, y2, paired = TRUE)

## 
##  Paired t-test
## 
## data:  y1 and y2
## t = 0.2388, df = 19, p-value = 0.8138
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.6600471  0.8300599
## sample estimates:
## mean of the differences 
##              0.08500641

Two-way ANOVA

# Fake data
n  <- 20
A1B1 <- rnorm(n)
A1B2 <- rnorm(n, 0.2)
A1B3 <- rnorm(n, -0.3)
A2B1 <- rnorm(n, 5)
A2B2 <- rnorm(n, -1)
A2B3 <- rnorm(n, 4)
Y    <- c(A1B1, A1B2, A1B3, A2B1, A2B2, A2B3)
A_factor  <- c(rep("A1", n*3), rep("A2", n*3))
B_factor  <- rep(c(rep("B1", n), rep("B2", n), rep("B3", n)), 2)
df        <- data.frame(Y = Y, A_factor = A_factor, B_factor = B_factor)

# Create design matrix
params <- 2 * 3
X <- matrix(0, ncol = params, nrow = n*params)
# Change first row to be the beta mean
X[, 1] <- 1
# Change the second row to be betaA1
X[, 2] <- rep(c(1, -1), each = nrow(X)/2)
# Change the third row to be betaB1
X[, 3] <- rep(rep(c(1, 0, -1), each = n), 2)
# Change the fourth row to be betaB2
X[, 4] <- rep(rep(c(0, 1, -1), each = n), 2)
# Change the fifth row to be betaA1B1
X[, 5] <- c(rep(c(1, 0, -1), each = n), rep(c(-1, 0, 1), each = n))
# Change the sixth row to be betaA1B2
X[, 6] <- c(rep(c(0, 1, -1), each = n), rep(c(0, -1, 1), each = n))

# Display design matrix
dispDesignMatrix(X)
title(main = '2 x 2 Anova design matrix')


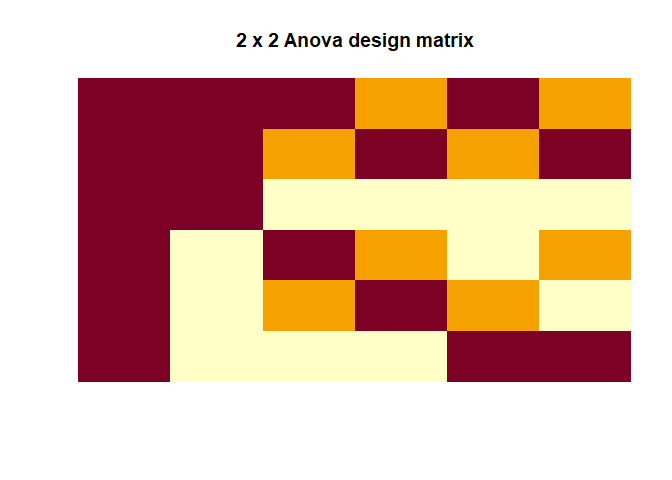
# Estimate betas
B <- solve(t(X)%*% X) %*% t(X) %*% Y

# Calculate residual variance
Y_hat <- X %*% B
E <- Y - Y_hat
p <- ncol(X)
N <- nrow(X)
resid_var <- as.numeric((t(E) %*% E)/(N-p))

# Covariance of beta
Cov_hat_beta <- solve(t(X) %*% X) * resid_var

# Contrasts & tests
# Con 1: Overall mean 
con1    <- matrix(c(1, 0, 0, 0 ,0 ,0), nrow = 1)
r       <- as.numeric(rankMatrix(con1))
F_stat1 <- t(con1 %*% B) %*% solve(r * con1 %*% Cov_hat_beta %*% t(con1)) %*% (con1 %*% B)

# Con 2: Main A effect
con2    <- matrix(c(0, 1, 0, 0 ,0 ,0), nrow = 1)
r       <- as.numeric(rankMatrix(con2))
F_stat2 <- t(con2 %*% B) %*% solve(r * con2 %*% Cov_hat_beta %*% t(con2)) %*% (con2 %*% B)

# Con 3: Main B effect
con3    <- rbind(c(0, 0, 1, 0 ,0 ,0), c(0, 0, 0, 1, 0, 0))
r       <- as.numeric(rankMatrix(con3))
F_stat3 <- t(con3 %*% B) %*% solve(r * con3 %*% Cov_hat_beta %*% t(con3)) %*% (con3 %*% B)

# Con 4: A/B interaction effect
con4    <- rbind(c(0, 0, 0, 0 ,1 ,0), c(0, 0, 0, 0, 0, 1))
r       <- as.numeric(rankMatrix(con4))
F_stat4 <- t(con4 %*% B) %*% solve(r * con4 %*% Cov_hat_beta %*% t(con4)) %*% (con4 %*% B)

# Con 5: Overall effect (any group difference)?
con5    <- diag(6)
con5    <- con5[-1,]
r       <- as.numeric(rankMatrix(con5))
F_stat5 <- t(con5 %*% B) %*% solve(r * con5 %*% Cov_hat_beta %*% t(con5)) %*% (con5 %*% B)

Again, we can compare this to what base R functions estimate:

res.aov <- aov(Y ~ A_factor  * B_factor, data = df)
summary(res.aov)

##                    Df Sum Sq Mean Sq F value Pr(>F)    
## A_factor            1  188.2  188.22  175.42 <2e-16 ***
## B_factor            2  161.5   80.77   75.27 <2e-16 ***
## A_factor:B_factor   2  220.7  110.37  102.86 <2e-16 ***
## Residuals         114  122.3    1.07                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

which fits with our $F$-values that we estimated 175.4229, 75.2738, 102.8615.

Does the contrast weighting matter for the test-statistics?

One thing I asked myself when thinking about it, is whether matters and if not why doesn’t it matter how we have weigh our contrast. Often we read that the contrast $con_1$ gives use the average of the two betas but is this true? Let’s look at this for two-sample $t$-test.

# Generate new data
y1 <- rnorm(n, 0)
y2 <- rnorm(n, 0.3)
Y  <- c(y1, y2)

# Create design matrix
X <- matrix(c(rep(c(1,0), each = n), rep(c(0,1), each = n)), ncol = 2)

# Estimate betas
B <- solve(t(X)%*% X) %*% t(X) %*% Y

# Calculate residual variance
Y_hat <- X %*% B
E <- Y - Y_hat
p <- ncol(X)
N <- nrow(X)
resid_var <- as.numeric((t(E) %*% E)/(N-p))

# Contrast
con1 <- matrix(c(1, 1), ncol = 2)
con2 <- matrix(c(0.5, 0.5), ncol = 2)

# Case 1
# Calculate the t value
numerator1   <- con1 %*% B
denominator1 <- sqrt(con1 %*% solve(t(X)%*% X) %*% t(con1) * resid_var)
t_value1     <- numerator1/denominator1

# Case 2
# Calculate the t value
numerator2   <- con2 %*% B
denominator2 <- sqrt(con2 %*% solve(t(X)%*% X) %*% t(con2) * resid_var)
t_value2     <- numerator2/denominator2

when we look at the numerator for $con_1$, which is supposed to represent the average of both $\beta$s we see that it is 0.164 but the average of $Y$ is only 0.082. So, in fact we get the average of the $\beta$s/groups times 2! We only actually get the true average when we use $con_2$ as a contrast, here the numerator is indeed 0.082. Does this actually matter for the test statistic? Well, no because as we scale the numerator by two, we also scale the denominator by the same amount and it cancels each other out. Both contrasts get exactly the same $t$-value of 0.565176.

Covariance matrix of the residuals

So, while reading through the Poldrack’s book I kind of stumbled over the concept of the covariance matrix of the residuals, which this is an important concept for time-series and heterogeneous variances but I didn’t really understand it when I am honest. So here I am trying to explore this:

The variance-covariance matrix is given by (in Kutner, 2005 this is written as $\sigma^2{\epsilon}$ and $MSE$ is used for estimation)

$$ \hat{Cov}(\hat{\epsilon}) = \sigma^2(I-H) $$

where $I$ is the identity matrix and $H$ is the so-called hat matrix that essentially can be used to transform $Y$ into $\hat{Y}$ directly (i.e. $\hat{Y} = HY$).

$$ H = X(X^\intercal X)^{-1}X^\intercal$$

Let’s calculate the covariance-variance matrix for our last example (the 2 x 2 ANOVA)

H         <- X %*% solve(t(X) %*% X) %*% t(X)
I         <- diag(nrow(H))
resid_cov <- resid_var * (I - H)

# Display design matrix
dispDesignMatrix(resid_cov)
title(main = 'Variance-covariance matrix for the 2 x 2 ANOVA example')

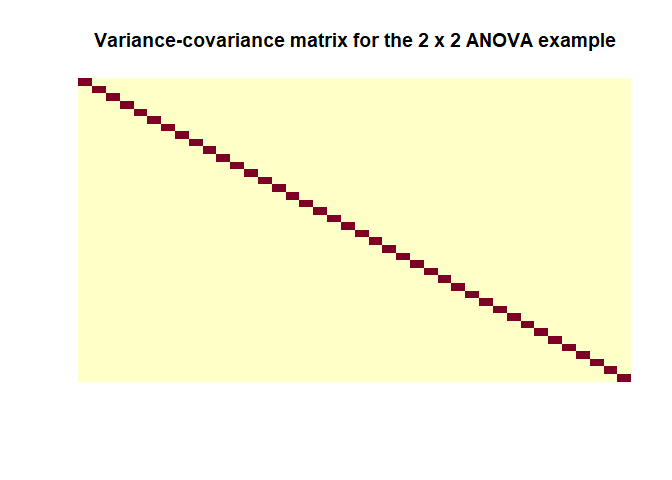
as when using the formula we can see $\hat{Cov}(\hat{\epsilon})$ is indeed a matrix with values close to zero off the diagonals and the a constant value on the diagonals. Important note: this estimation is only based on the design matrix $X$ so it doesn’t represent a feature of the data because we can’t really estimate the covariance of the true residuals so calculating this for your model will tell you nothing. It is simply an important assumption that is made about the data in order for everything to check out as intended. I found this helpful post about it.

A example design matrix for fMRI

The last thing directly related to the GLM that I wanted to explore is what first-level fMRI GLMs typically look like. That is because the actual design matrix used when fitting a GLM to fMRI data are the regressors (i.e. time points) convolved with the HRF. This is based on explanations and code from Jeanette Mumford (video & code). Here I illustrate constructing regressors for an first-level fMRI analysis. Note that in principle you want to convolve your events (onset + duration) with the HRF at a higher temporal resolution but for what ever reason this doesn’t seem to work well with the package that I am using. (Update: This is soon to be fixed by the developers.)

# Libs
library(fmri)

# Input parameters
TR_conv    <- 1 
numOfScans <- 100
numEvents1 <- 20
numEvents2 <- 20
duration1  <- 2/TR_conv   # in scans
duration2  <- 1.5/TR_conv # in scans
  
# Calculated parameters based on input
onsets1   <- sample(1:numOfScans, numEvents1) # Onset in scans
onsets2   <- sample(1:numOfScans, numEvents2) # Onset in scans
duration1 <- rep(duration1, length(onsets1))
duration2 <- rep(duration2, length(onsets2))

# Create regressors
regressor1 <- fmri.stimulus(numOfScans, onsets1, duration1, TR_conv)
regressor2 <- fmri.stimulus(numOfScans, onsets2, duration2, TR_conv)

The results can be visualised as

# Visualiation libs
library(ggplot2)
library(cowplot)

# Create DFs
df1_events <- data.frame(onsets = onsets1, duration = duration1)
df2_events <- data.frame(onsets = onsets2, duration = duration2)
df1_BOLD   <- data.frame(scans = 1:length(regressor1), Regressor = regressor1) 
df2_BOLD   <- data.frame(scans = 1:length(regressor2), Regressor = regressor2) 

# Plots
stickPlot1 <- ggplot(df1_events) + 
  geom_rect(mapping = aes(xmin = onsets, xmax = onsets + duration, ymin = 0, ymax = 1)) + 
  theme(axis.ticks.y = element_blank(), axis.text.y = element_blank()) + 
  labs(x = "Scans") + 
  coord_cartesian(xlim = c(1, length(regressor1)))

stickPlot2 <- ggplot(df2_events) + 
  geom_rect(mapping = aes(xmin = onsets, xmax = onsets + duration, ymin = 0, ymax = 1)) + 
  theme(axis.ticks.y = element_blank(), axis.text.y = element_blank()) + 
  labs(x = "Scans") + 
  coord_cartesian(xlim = c(1, length(regressor2)))

BOLD_plot1 <- ggplot(df1_BOLD, aes(x = scans, y = Regressor)) + geom_line() + labs(x = "") + 
  coord_cartesian(xlim = c(1, length(regressor1)))

BOLD_plot2 <- ggplot(df2_BOLD, aes(x = scans, y = Regressor)) + geom_line() + labs(x = "") + 
  coord_cartesian(xlim = c(1, length(regressor2)))

# Combination
plot_grid(BOLD_plot1, BOLD_plot2, stickPlot1, stickPlot2, align = "v")

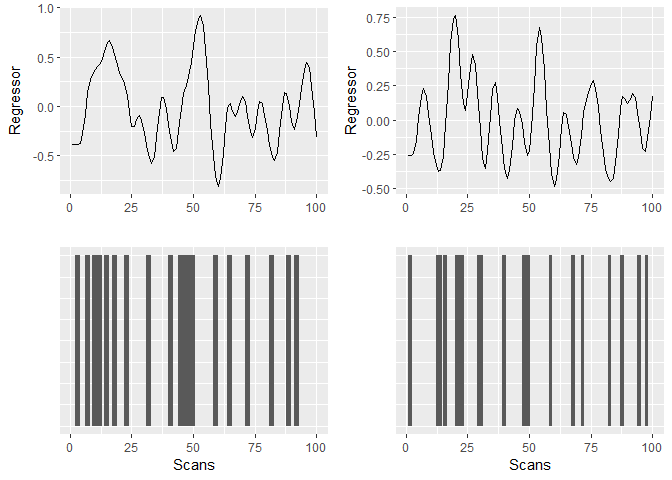
The resulting design matrix as used for fMRI would look like this

# Create design matrix
X <- matrix(c(rep(1, length(regressor1)), regressor1, regressor2), ncol = 3)

# Display design matrix
dispDesignMatrix(X)
title(main = 'Design matrix based on convolutation with HRF')

This, in other words a simple multiple regression model with continuous regressors, is what actually would be used to model the brain responses (at least for the first level analysis). Again, this ignores the problem of auto-correlation in the time-series and that the assumption about the covariance variance matrix of the residuals would not hold without extra steps, which are ignored here.

Multiple testing problem

The last problem I looked is not really GLM specific but important for fMRI analyses. When doing mass-univariate statistics on the brain, this usually means that we in fact run more than 100,000 individual tests as at least one test is run per voxel in the brain image. This is illustrated with this example of 2D fake brain image:

# Seed
set.seed(10)

# Create smoothed image
numberOfVoxels      <- 316*316
brainImage          <- matrix(rnorm(numberOfVoxels), ncol = sqrt(numberOfVoxels))
brainImage_smoothed <- gaussianSmooth2D(brainImage, kernelSize = 3, kernelSD = 0.6)

# Significant values etc
cutoff    <- qnorm(0.05/2) # Cut off value for 95 % for two-tailed test
sig_num1  <- sum(brainImage < cutoff | brainImage > -cutoff)
sig_num2  <- sum(brainImage_smoothed < cutoff | brainImage_smoothed > -cutoff)
sig_rate1 <- mean(brainImage < cutoff | brainImage > -cutoff)
sig_rate2 <- mean(brainImage_smoothed < cutoff | brainImage_smoothed > -cutoff)

# Threshold the image
brainImage_smoothed_threshold <- brainImage_smoothed
brainImage_smoothed_threshold[brainImage_smoothed_threshold > cutoff & brainImage_smoothed_threshold < -cutoff] <- NA

# Plot
plot_grid(levelplot(brainImage_smoothed), levelplot(brainImage_smoothed_threshold))

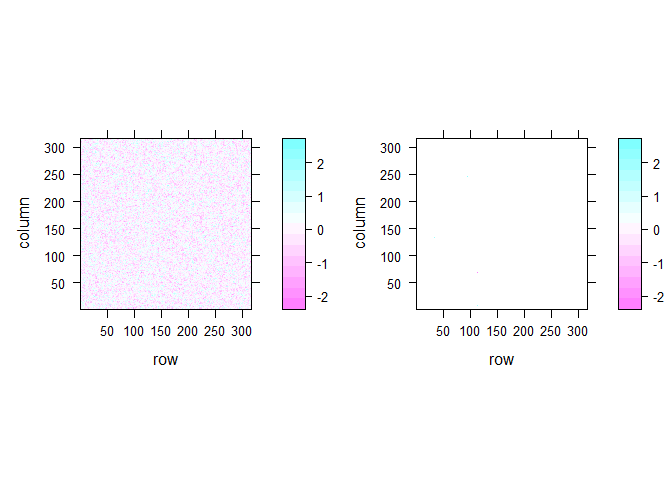
Even if there is no true effect, there are quite a number of significant voxels in that 2D brain image even when I smoothed it (13 voxel). In the unsmoothed image, we get a number of significant cases that is pretty much expected given the number of tests that we simulated (5060 voxels or 5.07 %). In real fMRI the false positive rate is obviously not that bad because voxels are not actually independent but it is still an important issue.

Note I am only discussing voxel-wise corrections but many of the concepts below also work for cluster level.

Calculate FWE

As defined below, FWE = chance of 1 more significant voxels in the brain and we want that to be 5%. So how much is the FWE in my completely fictional example for smoothed image.

# Simulation parameters
cutoff <- qnorm(0.05/2) # Cut off value for 95 % for two-tailed test
nSim   <- 10000

# Function to calculate FWE and create max distribution (see below)
simFun <- function(numberOfVoxels, cutoff){
  # Create random smooth image
  brainImage          <- matrix(rnorm(numberOfVoxels), ncol = sqrt(numberOfVoxels))
  brainImage_smoothed <- gaussianSmooth2D(brainImage, kernelSize = 3, kernelSD = 0.6)
  
  # Calculate number of significant voxels
  sig_num   <- sum(brainImage_smoothed < cutoff | brainImage_smoothed > -cutoff)
  max_value <- max(abs(brainImage_smoothed))
  
  return(c(sig_num, max_value))
}

# Save results in here
sim_results <- matrix(rep(c(NA,NA), each = nSim), ncol = 2)

# Loop for simulation
for(i in 1:nSim){
  sim_results[i, ] <- simFun(numberOfVoxels, cutoff)
}

Even with this relatively low number of significant voxels in each smoothed image the FWE is very high with 99.9 %.

FWE correction

As noted elsewhere Bonferroni is far too conservative. Two alternatives to correct for the FWE rates are random field theory (RFT) & permutation testing.

Random field theory

Famously, RFT is quite complex so I am not trying to dive much deeper into this matter other than repeating an equation taken out of Poldrack et al. (2011):

$$p_{FWE}^{vox} \approx R \times \frac{(4ln(2))^{3/2}}{(2\pi)^2}e^{-t^2/2}(t^2-1)$$

where $R = V/(FWHM_xFWHM_yFWHM_z)$ (RESolution ELement aka RESEL) and $V$ is the search volume.

Permutation tests

Permutation tests are something that can be relatively easily be simulated. This can be done by creating a number of brain images and saving the max-value test statistic in this image. I already did this while calculating the FWE above.

ggplot(data.frame(z = sim_results[, 2]), aes(x = z)) + 
  geom_histogram(bins = 100) +
  labs(x = "Z-value", y = "Count", title = "Distribution of maximal absolute Z value")

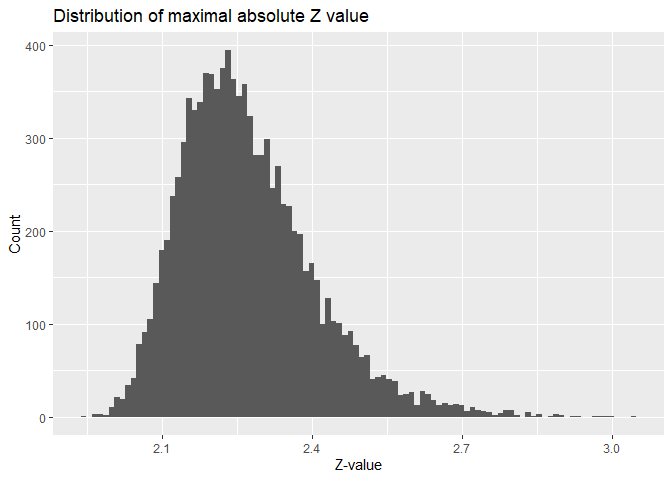
The FWE-corrected $p$-value is simply the percentage of values that are larger than our test statistic in that distribution. Take for example a z-value of 2.2025748. The $p$-values are as follows:

  • Uncorrected: 0.0276247
  • Bonferroni corrected: 1 (the $\alpha$-level would be 5.0072104^{-7}). In other words, we would only count absolute z-values of 5.0260363 or higher as significant.
  • Permutation corrected: 0.3366. Here we would count values of at least 2.5175497 as significant.

FDR

Another way to correct the p-value is using FDR for instance using Benjamini’s & Hochberg’s proecdure. To simulate this, we again take our fake 2D brain image and convert the z-values into p-values.

zMap <- brainImage_smoothed
pMap <- (1-pnorm(abs(zMap)))*2

As a reminder, we have 13 voxels that are deemed significant. In Step 1 we have to sort our p-values from smallest to largest and assign a rank.

FDR_df <- data.frame(p = sort(pMap), rank = 1:length(pMap))

for Step 2 we calculate the critical value for each p-value using

$$ crit = (i/m)\times Q $$

  • $i$ = rank of p-value
  • $m$ = total number of tests
  • $Q$ = your chosen false discovery rate, which we set to 0.05.
# Parameters for critical value calculation
m <- numberOfVoxels
Q <- 0.05

# Calculation itself
FDR_df$crit <- (FDR_df$rank/m) * Q

Step 3 we try to find row where the value of the p-value is lower than the critical value.

FDR_df$lower <- FDR_df$p < FDR_df$crit

In this case, any(FDR_df$lower) is FALSE. Finally for adjusting a p-value according to this procedure we can use this formula that I found:

p^\mathrm{BH}{(i)} = \min\Big\{\min{j\gei}\big\{\frac{mp_{(j)}}{j}\big\},1\Big}

FDR_df$adjusted <- ifelse((FDR_df$p*m)/FDR_df$rank > 1, 1, (FDR_df$p*m)/FDR_df$rank)
# Then check if completely decreasing
for(i in nrow(FDR_df):2){
  if(FDR_df$adjusted[i] < FDR_df$adjusted[i - 1]){
    FDR_df$adjusted[i - 1] <- FDR_df$adjusted[i]
  }
}

This adjustment makes all our p-values 1. In more interesting example, we get this:

ps     <- runif(10)
ps     <- c(0.001, ps)
FDR_df <- data.frame(p = sort(ps), rank = 1:length(ps))

m <- length(ps)
Q <- 0.05

# Calculation itself
FDR_df$crit <- (FDR_df$rank/m) * Q
FDR_df$lower <- FDR_df$p < FDR_df$crit
FDR_df$adjust_manual  <- ifelse((FDR_df$p*m)/FDR_df$rank > 1, 1, (FDR_df$p*m)/FDR_df$rank)
# Then check if completely decreasing
for(i in nrow(FDR_df):2){
  if(FDR_df$adjust_manual[i] < FDR_df$adjust_manual[i - 1]){
    FDR_df$adjust_manual[i - 1] <- FDR_df$adjust_manual[i]
  }
}
FDR_df$adjust_adjust  <- p.adjust(sort(ps), method = "BH")

# Display table
kable(FDR_df)
p rank crit lower adjust_manual adjust_adjust
0.0010000 1 0.0045455 TRUE 0.0110000 0.0110000
0.0075637 2 0.0090909 TRUE 0.0416003 0.0416003
0.1600754 3 0.0136364 FALSE 0.3877979 0.3877979
0.1727596 4 0.0181818 FALSE 0.3877979 0.3877979
0.1762718 5 0.0227273 FALSE 0.3877979 0.3877979
0.2380772 6 0.0272727 FALSE 0.4364749 0.4364749
0.4092754 7 0.0318182 FALSE 0.5036225 0.5036225
0.4096089 8 0.0363636 FALSE 0.5036225 0.5036225
0.4120547 9 0.0409091 FALSE 0.5036225 0.5036225
0.6297573 10 0.0454545 FALSE 0.6927330 0.6927330
0.9008737 11 0.0500000 FALSE 0.9008737 0.9008737

Conclusion

Overall, I have to say that despite having dealt with these kind of questions & problems for years only really playing around with the equations in code helped me understand the concepts in deeper way. Hopefully, other people might also find this somewhat useful.

Glossary

  • Rank = Number of independent columns in matrix or the number of dimensions in the output (if matrices are seen as transformations).
  • Full rank = Rank is as high as the number of columns.
  • FWE (rate) = “is the chance of one or more false positives anywhere in the image.” (Poldrack et al., 2011, p. 117)
  • Bonferroni = A correction where simply $\frac{\alpha}{number\ of\ tests}$ assuming the the tests are independent. This is a method to correct FWE.
  • FDR = Expected proportion of voxels deemed significant that are false positives.

Share